Они не больны так как у них нет повышенной температуры логика
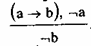
ÐолÑÑиÑÑ Ð²ÑполненнÑÑ ÑабоÑÑ Ð¸Ð»Ð¸ конÑÑлÑÑаÑÐ¸Ñ ÑпеÑиалиÑÑа по ваÑемÑ
ÑÑÐµÐ±Ð½Ð¾Ð¼Ñ Ð¿ÑоекÑÑ
УзнаÑÑ ÑÑоимоÑÑÑ
ÐÑделиÑе иÑÑ Ð¾Ð´Ð½ÑÑ Ð¼ÑÑÐ»Ñ (ÑезиÑ) и аÑгÑменÑÑ (оÑнованиÑ) в пÑиведеннÑÑ Ð½Ð¸Ð¶Ðµ ÑаÑÑÑждениÑÑ Ð¸ опÑеделиÑе, наÑÑÑен ли в Ð½Ð¸Ñ Ð·Ð°ÐºÐ¾Ð½ доÑÑаÑоÑного оÑнованиÑ.
1. ÐÑи две пÑÑмÑе паÑаллелÑнÑ, поÑколÑÐºÑ Ñ Ð½Ð¸Ñ Ð½ÐµÑ Ð¾Ð±ÑÐ¸Ñ ÑоÑек.
Рданном ÑаÑÑÑждении ÑÐµÐ·Ð¸Ñ – две пÑÑмÑе паÑаллелÑнÑ, а оÑнование – Ñ Ð½Ð¸Ñ Ð½ÐµÑ Ð¾Ð±ÑÐ¸Ñ ÑоÑек, закон доÑÑаÑоÑного оÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð½Ðµ наÑÑÑен.
2. ÐÑи две пÑÑмÑе паÑаллелÑнÑ, Ñ.к. они Ð»ÐµÐ¶Ð°Ñ Ð² одной плоÑкоÑÑи и не имеÑÑ Ð¾Ð±ÑÐ¸Ñ ÑоÑек.
Рданном ÑаÑÑÑждении ÑÐµÐ·Ð¸Ñ – две пÑÑмÑе паÑаллелÑнÑ, а оÑнование – Ñ Ð½Ð¸Ñ Ð½ÐµÑ Ð¾Ð±ÑÐ¸Ñ ÑоÑек, закон доÑÑаÑоÑного оÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð½Ðµ наÑÑÑен.
3. Ðанное веÑеÑÑво ÑвлÑеÑÑÑ Ð¼ÐµÑаллом, поÑÐ¾Ð¼Ñ ÑÑо оно ÑлекÑÑопÑоводно.
Рданном ÑаÑÑÑждении ÑÐµÐ·Ð¸Ñ – данное веÑеÑÑво ÑвлÑÑÑÑÑ Ð¼ÐµÑаллом, а оÑнование – оно ÑлекÑÑопÑоводно, закон доÑÑаÑоÑного оÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð½Ð°ÑÑÑен, поÑÐ¾Ð¼Ñ ÑÑо еÑли веÑеÑÑво ÑлекÑÑопÑоводно, ÑÑо не знаÑÐ¸Ñ ÑÑо оно ÑвлÑеÑÑÑ Ð¼ÐµÑаллом.
4. Ðой ÑоваÑÐ¸Ñ «Ð·Ð°ÑабаÑÑваеѻ $10000 в меÑÑÑ, в Ñем нелÑÐ·Ñ ÑÑомниÑÑÑÑ, Ð²ÐµÐ´Ñ Ð¾Ð½ Ñам ÑÑо ÑÑвеÑждаеÑ.
Рданном ÑаÑÑÑждении ÑÐµÐ·Ð¸Ñ – мой ÑоваÑÐ¸Ñ «Ð·Ð°ÑабаÑÑваеѻ $10000 в меÑÑÑ, оÑнование – он Ñам ÑÑо ÑÑвеÑждаеÑ. Ðакон доÑÑаÑоÑного оÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð½Ð°ÑÑÑен, поÑÐ¾Ð¼Ñ ÑÑо Ð½ÐµÑ Ð´Ð¾ÐºÐ°Ð·Ð°ÑелÑÑÑв, ÑÑо ÑоваÑÐ¸Ñ ÑÑвеÑÐ¶Ð´Ð°ÐµÑ Ð¿ÑавдÑ, он Ð¼Ð¾Ð¶ÐµÑ Ð³Ð¾Ð²Ð¾ÑиÑÑ Ð¸ непÑавдÑ. СказаÑÑ Ð¼Ð¾Ð¶Ð½Ð¾ вÑе ÑÑо Ñгодно.
5. Родном амеÑиканÑком ÑÑаÑе поÑеÑпела кÑÑÑение леÑаÑÑÐ°Ñ ÑаÑелка, Ð²ÐµÐ´Ñ Ð¾Ð± ÑÑом пиÑали в газеÑÐ°Ñ , ÑÑо пеÑедавали по Ñадио и даже показÑвали по ÑелевидениÑ.
Рданном ÑаÑÑÑждении ÑÐµÐ·Ð¸Ñ – в амеÑиканÑком ÑÑаÑе поÑеÑпела кÑÑÑение леÑаÑÑÐ°Ñ ÑаÑелка, а оÑнование – об ÑÑом пиÑали в газеÑÐ°Ñ , говоÑили по Ñадио, показÑвали по ÑелевидениÑ. Ðакон доÑÑаÑоÑного оÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð½Ð°ÑÑÑен, поÑÐ¾Ð¼Ñ ÑÑо Ð½ÐµÑ Ð´Ð¾ÐºÐ°Ð·Ð°ÑелÑÑÑв, ÑÑо леÑаÑÑÐ°Ñ ÑаÑелка пÑавда поÑеÑпела кÑÑÑение в амеÑиканÑком ÑÑаÑе, Ñ.к. в газеÑÐ°Ñ , по Ñадио и по ÑÐµÐ»ÐµÐ²Ð¸Ð´ÐµÐ½Ð¸Ñ Ð½Ðµ вÑегда говоÑÑÑ Ð¿ÑавдÑ. СказаÑÑ Ð¼Ð¾Ð¶Ð½Ð¾ вÑе ÑÑо Ñгодно.
6. Ð¡ÐµÐ³Ð¾Ð´Ð½Ñ ÐºÐ¾Ñабли не могÑÑ Ð·Ð°Ñ Ð¾Ð´Ð¸ÑÑ Ð² бÑÑ ÑÑ, поÑÐ¾Ð¼Ñ ÑÑо она заминиÑована.
Рданном ÑаÑÑÑждении ÑÐµÐ·Ð¸Ñ – ÑÐµÐ³Ð¾Ð´Ð½Ñ ÐºÐ¾Ñабли не могÑÑ Ð·Ð°Ñ Ð¾Ð´Ð¸ÑÑ Ð² бÑÑ ÑÑ, а оÑнование – она заминиÑована. Ðакон доÑÑаÑоÑного оÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð½Ðµ наÑÑÑен.
7. ÐÑÐ¾Ñ Ñеловек не болен, Ð²ÐµÐ´Ñ Ñ Ð½ÐµÐ³Ð¾ не повÑÑена ÑемпеÑаÑÑÑа.
Рданном ÑаÑÑÑждении ÑÐµÐ·Ð¸Ñ – ÑÑÐ¾Ñ Ñеловек не болен, а оÑнование – Ñ Ð½ÐµÐ³Ð¾ не повÑÑена ÑемпеÑаÑÑÑа. Ðакон доÑÑаÑоÑного оÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð½Ð°ÑÑÑен, поÑÐ¾Ð¼Ñ ÑÑо можно болеÑÑ Ð¸ ÑемпеÑаÑÑÑа Ð¼Ð¾Ð¶ÐµÑ Ð±ÑÑÑ Ð½Ðµ повÑÑенной.
8. Ðанное Ñлово надо пиÑаÑÑ Ñ Ð±Ð¾Ð»ÑÑой бÑквÑ, Ñ.к. оно ÑÑÐ¾Ð¸Ñ Ð² наÑале пÑедложениÑ.
Рданном ÑаÑÑÑждении ÑÐµÐ·Ð¸Ñ – данное Ñлово надо пиÑаÑÑ Ñ Ð±Ð¾Ð»ÑÑой бÑквÑ, а оÑнование – оно ÑÑÐ¾Ð¸Ñ Ð² наÑале пÑедложениÑ. Ðакон доÑÑаÑоÑного оÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð½Ðµ наÑÑÑен.
9. «…Ð¢Ñ Ð²Ð¸Ð½Ð¾Ð²Ð°Ñ Ñж Ñем, ÑÑо Ñ Ð¾ÑеÑÑÑ Ð¼Ð½Ðµ кÑÑаÑÑ» (Ð.Ð.ÐÑÑлов «Ðолк и Ñгненок»).
Рданном ÑаÑÑÑждении ÑÐµÐ·Ð¸Ñ – ÑÑ Ð²Ð¸Ð½Ð¾Ð²Ð°Ñ, а оÑнование – Ñ Ð¾ÑеÑÑÑ Ð¼Ð½Ðµ кÑÑаÑÑ. Ðакон доÑÑаÑоÑного оÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð½Ð°ÑÑÑен, поÑÐ¾Ð¼Ñ ÑÑо еÑли кÑо Ñо Ñ Ð¾ÑÐµÑ ÐµÑÑÑ, ÑÑо не доказÑваеÑ, ÑÑо в ÑÑом Ð²Ð¸Ð½Ð¾Ð²Ð°Ñ ÐºÑо Ñо дÑÑгой.
10. Ðода ÑÑÑÐ¸Ñ Ð¾Ð³Ð¾Ð½Ñ, поÑÐ¾Ð¼Ñ ÑÑо она Ð¶Ð¸Ð´ÐºÐ°Ñ Ð¸ Ñ Ð¾Ð»Ð¾Ð´Ð½Ð°Ñ.
Рданном ÑаÑÑÑждении ÑÐµÐ·Ð¸Ñ – вода ÑÑÑÐ¸Ñ Ð¾Ð³Ð¾Ð½Ñ, а оÑнование – она Ð¶Ð¸Ð´ÐºÐ°Ñ Ð¸ Ñ Ð¾Ð»Ð¾Ð´Ð½Ð°Ñ. Ðакон доÑÑаÑоÑного оÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð½Ðµ наÑÑÑен.
11. ÐÐµÐ¼Ð»Ñ Ð¸ СолнÑе ÑÑаÑÑвÑÑÑ Ð² гÑавиÑаÑионном взаимодейÑÑвии, поÑколÑÐºÑ Ð¾Ð½Ð¸ ÑвлÑÑÑÑÑ Ð¾Ð±ÑекÑами мегамиÑа, а вÑе обÑекÑÑ Ð¼ÐµÐ³Ð°Ð¼Ð¸Ñа ÑÑаÑÑвÑÑÑ Ð² гÑавиÑаÑионном взаимодейÑÑвии.
Рданном ÑаÑÑÑждении ÑÐµÐ·Ð¸Ñ – ÐÐµÐ¼Ð»Ñ Ð¸ СолнÑе ÑÑаÑÑвÑÑÑ Ð² гÑавиÑаÑионном взаимодейÑÑвии, а оÑнование – они ÑвлÑÑÑÑÑ Ð¾Ð±ÑекÑами мегамиÑа, а вÑе обÑекÑÑ Ð¼ÐµÐ³Ð°Ð¼Ð¸Ñа ÑÑаÑÑвÑÑÑ Ð² гÑавиÑаÑионном взаимодейÑÑвии. Ðакон доÑÑаÑоÑного оÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð½Ðµ наÑÑÑен.
12. СÑÑденÑÑ Ð¡ÑепаÑÐºÐ¸Ð½Ñ ÑледÑÐµÑ Ð¿Ð¾ÑÑавиÑÑ Ð·Ð°ÑеÑ, Ñак как он ÑÐµÐ·Ð¶Ð°ÐµÑ Ð½Ð° ÑоÑÐµÐ²Ð½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð¿Ð¾ баÑкеÑболÑ.
Рданном ÑаÑÑÑждении ÑÐµÐ·Ð¸Ñ – ÑÑÑденÑÑ Ð¡ÑепаÑÐºÐ¸Ð½Ñ ÑледÑÐµÑ Ð¿Ð¾ÑÑавиÑÑ Ð·Ð°ÑеÑ, а оÑнование – он ÑÐµÐ·Ð¶Ð°ÐµÑ Ð½Ð° ÑоÑÐµÐ²Ð½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð¿Ð¾ баÑкеÑболÑ. Ðакон доÑÑаÑоÑного оÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð½Ð°ÑÑÑен, поÑÐ¾Ð¼Ñ ÑÑо еÑли СÑепаÑкин ÑÐµÐ·Ð¶Ð°ÐµÑ Ð½Ð° ÑоÑÐµÐ²Ð½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð¿Ð¾ баÑкеÑÐ±Ð¾Ð»Ñ ÑÑо не доказÑваеÑ, ÑÑо он Ð·Ð½Ð°ÐµÑ Ð¿ÑÐµÐ´Ð¼ÐµÑ Ð¿Ð¾ коÑоÑÐ¾Ð¼Ñ ÐµÐ¼Ñ ÑледÑÐµÑ Ð¿Ð¾ÑÑавиÑÑ Ð·Ð°ÑеÑ.
13. Ð, кÑÑаÑи, ÑлÑÑали? ÐÑеÑа ÑÑанÑÐµÑ ÑÑли,
Так оÑкопали две конÑÑÑнÑе ÑÑÑÑи!
ÐовоÑÑÑ, ÑÐ¿Ð¸Ð¾Ð½Ñ Ð²Ð¾Ð´Ñ Ñамогоном оÑÑавили,
ÐÑ Ð° Ñ Ð»ÐµÐ± ÑепеÑÑ Ð¸Ð· ÑÑбÑей ÑеÑÑи!
Ð, кÑÑаÑи, ÑлÑÑали? ÐамÑкина ÑнимаÑÑ —
Ðа ÑазвÑÐ°Ñ ÐµÐ³Ð¾, за пÑÑнкÑ, за дебоÑ!
Ð, кÑÑаÑи, ваÑего ÑоÑеда, негодÑÑ, забиÑаÑÑ,
ÐоÑÐ¾Ð¼Ñ ÑÑо он на ÐеÑÐ¸Ñ Ð¿Ð¾Ñ Ð¾Ð¶!
Ð.С. ÐÑÑоÑкий «Ð¡Ð»ÑÑ Ð¸»
Рданном ÑаÑÑÑждении ÑÐµÐ·Ð¸Ñ – оÑкапали две конÑÑÑнÑе ÑÑÑÑи, а оÑнование – ÑÐ¿Ð¸Ð¾Ð½Ñ Ð²Ð¾Ð´Ñ Ñамогоном оÑÑавили. Ðакон доÑÑаÑоÑного оÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð½Ð°ÑÑÑен, поÑÐ¾Ð¼Ñ ÑÑо ÑÐµÐ·Ð¸Ñ Ð½Ðµ вÑÑÐµÐºÐ°ÐµÑ Ð¸Ð· оÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ñ Ð½ÐµÐ¾Ð±Ñ Ð¾Ð´Ð¸Ð¼Ð¾ÑÑÑÑ. Ð¤Ð°ÐºÑ Ñого ÑÑо ÑÐ¿Ð¸Ð¾Ð½Ñ Ð¾ÑÑавили Ð²Ð¾Ð´Ñ Ñамогоном, не доказÑваеÑ, ÑÑо оÑкапали две конÑÑÑнÑе ÑÑÑÑи.
Рданном ÑаÑÑÑждении ÑÐµÐ·Ð¸Ñ – ÐамÑкина ÑнимаÑÑ, а оÑнование – за ÑазвÑаÑ, за пÑÑнкÑ, за дебоÑ. Ðакон доÑÑаÑоÑного оÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð½Ðµ наÑÑÑен.
Рданном ÑаÑÑÑждении ÑÐµÐ·Ð¸Ñ – ваÑего ÑоÑеда, негодÑÑ, забиÑаÑÑ, а оÑнование – поÑÐ¾Ð¼Ñ ÑÑо он на ÐеÑÐ¸Ñ Ð¿Ð¾Ñ Ð¾Ð¶. Ðакон доÑÑаÑоÑного оÑÐ½Ð¾Ð²Ð°Ð½Ð¸Ñ Ð½Ð°ÑÑÑен, поÑÐ¾Ð¼Ñ ÑÑо еÑли ÑоÑед Ð¿Ð¾Ñ Ð¾Ð¶ на ÐеÑиÑ, ÑÑо не доказÑваеÑ, ÑÑо он негодÑй и его надо забиÑаÑÑ.
Ðнимание!
ÐÑли вам нÑжна помоÑÑ Ð² напиÑании ÑабоÑÑ, Ñо ÑекомендÑем обÑаÑиÑÑÑÑ Ðº
пÑоÑеÑÑионалам. Ðолее 70 000 авÑоÑов гоÑÐ¾Ð²Ñ Ð¿Ð¾Ð¼Ð¾ÑÑ Ð²Ð°Ð¼ пÑÑмо ÑейÑаÑ. ÐеÑплаÑнÑе
коÑÑекÑиÑовки и доÑабоÑки. УзнайÑе ÑÑоимоÑÑÑ Ñвоей ÑабоÑÑ.
Источник
Подобный материал:
- Реферат: Самоконтроль занимающихся физическими упражнениями и спортом, 305.08kb.
- Статья тема: «организация самостоятельных занятий физическими упражнениями», 201.91kb.
- План Характеристика нагрузок при занятиях физическими упражнениями Утомление и его, 197.51kb.
- Справочное пособие по грамматике с упражнениями для студентов 3-5 курсов Гомель 2005, 868.89kb.
- Реферат Тема: «Основы методики и организация самостоятельных занятий физическими упражнениями», 229.98kb.
- Абстракции, наследование и полиморфизм, 107.42kb.
- Название Стр, 3395.7kb.
- «Диагностика и самодиагностика состояния организма при регулярных занятиях физическими, 162.84kb.
- М. К. Аммосова рабочая программа, 97.59kb.
- Сестринское дело в терапии с курсом первичной медицинской помощи, 623.76kb.
^ ГЛАВА II. ПРОБЛЕМА ВЫВОДА В ЛОГИКЕ ВЫСКАЗЫВАНИЙ
§ 1. Схемы Хрисиппа
Все, что мы делали до сих пор, еще не может называться логикой в подлинном смысле этого слова. Ведь мы только вычисляли значение истинности одного высказывания в зависимости от истинности других. А выводов никаких не делали. Логика же должна иметь дело прежде всего с выводом одних мыслей (здесь — высказываний) из других мыслей.
Однако, мы уже создали аппарат, с помощью которого нетрудно построить теорию, дающую возможность отличить правильные выводы из данных высказываний от неправильных.
Что значит правильный вывод? Это совсем не означает, что полученное высказывание истинно само по себе. Например, мы можем рассуждать так. Известно, что имеет место а b и оказывается, что высказывание b — истинно. Значит, полагаем мы, истинным является высказывание а. Хорошо ли мы рассуждаем?
Приведем конкретный пример рассуждения, удовлетворяющего приведенной формуле. Если у человека повышенная температура, то он болен. Этот человек болен. Значит, у него повышенная температура. Проверяем. На самом деле, у него температура повышена. И мы думаем, что рассуждаем хорошо. Но так ли это? Запишем схему нашего рассуждения. Для этого отделим те мысли, из которых мы исходили, т. е. такие, истинность которых нам известна заранее, от той мысли, которую мы получаем, т. е. истинность которой определяется с помощью нашего рассуждения. Первое мы назовем
посылками,
а второе — выводом. Процесс же получения вывода на основе посылок будем называть умозаключением.
Представим умозаключение в виде схемы, в которой посылки будем записывать сверху черты, а вывод — под чертой. Применительно к нашему умозаключению, эта схема будет иметь вид:
Если у человека повышена температура, он болен.
^ Этот человек болен.
______
У него повышена температура.
Мы уже знаем, что у больного человека, назовем его Петровым, на самом деле температура повышена. А могла бы она не быть повышена при том же условии, т. е. при том, что Петров болен? Для ответа на этот вопрос нужно знать, бывают ли болезни, не сопровождающиеся повышением температуры. Мы можем и не знать этого, несмотря на то, что уверены в истинности наших посылок. Значит, истинность посылок в нашем примере не гарантирует истинности вывода. А если бы мы рассуждали правильно? Тогда
при условии истинности посылок вывод обязательно был бы истинным.
Для того, чтобы быть уверенным в истинности вывода, нам не нужно было бы ничего знать, кроме истинности посылок.
Можно ли убедиться в ошибочности умозаключения с помощью чисто формальных методов? Да. Для этого мы воспользуемся уже хорошо известными нам таблицами истинности. Построим таблицу истинности для a, b и а b, с помощью которой можно будет выяснить, могла ли быть такая ситуация, когда (а b) и b были бы истинными, но а, тем не менее, — ложным.
Табл. 20

Обратим внимание на 3-ю строчку нашей таблицы. Мы видим, что здесь (а b) истинно и b — истинно, но а, тем не менее, — ложно. Таким образом, выяснилась возможность ложного вывода при наличии истинных посылок. Это никуда не годится! Мы обнаружили ложность вывода о высокой температуре Петрова, не заглядывая ни в какие медицинские справочники, руководствуясь только таблицами истинности.
А какое умозаключение было бы правильным? Правильным было бы такое умозаключение: если у человека повышена температура, то он болен. У Петрова повышена температура. Значит, он болен.
Этому умозаключению соответствует следующая формула:
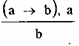
Проверим этот вывод с помощью нашей таблицы. В каком случае истинным является а и (а b)? Только в первой строчке, и именно в этом случае будет истинным b.
Мы привели одну из форм умозаключений, которые были сформулированы еще древнегреческим философом-стоиком Хрисиппом1. Он выражал его в форме:
I. Если есть А, то есть и В
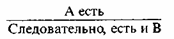
Кроме этой формы, у Хрисиппа были еще четыре типа умозаключений.
II. Если есть А, есть и В

Первая и вторая формы получили впоследствии название условно-категорических силлогизмов. Первая форма — утверждающий модус (Ponens), вторая — отрицающий модус (Tollens). Импликация (условное суждение) называется большей посылкой. Элементарные высказывания — меньшей посылкой.
III. Может быть или А, или
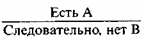
IV. Может быть или А, или В

Третья и четвертая формы называются разделительно-категорическими силлогизмами. Дизъюнкция называется большой посылкой, а элементарное высказывание в посылках — меньшей посылкой. Третья форма — утверждающе-отрицающий модус (Ропепdo-tollens), четвертая — отрицающе-утверждающий модус (Tollendo ponens).
V. А и В не могут быть вместе
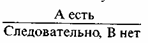
В нашей символике четыре типа умозаключений Хрисиппа (I-IV) выразятся следующим образом:
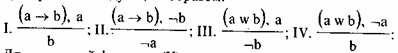
Для последней формулы (V) у нас нет знака. Мы ее не проходили. Такое отношение мы не изучали, но это не беда. Мы легко можем построить таблицу для посылки, используемой Хрисиппом. И если она обнаружится в составе нашей большой таблицы (Табл. 11), то это будет означать, что мы ее уже предусмотрели.
Что значит, что а и b не могут быть вместе? Это значит, что они не могут быть вместе истинными. Если хотя бы одно утверждение — а или b ложно, то истинно, что а и b не могут быть вместе.
В таблице это отобразится так:
Табл. 21

Наша связка новая, но она, естественно, не нова в логике. И в ней имеет свое название. Она называется штрих Шеффера и обозначается так: а/b.
Мы можем найти соответствующую связку в нашей большой таблице 11. Это колонка № 5. Нетрудно заметить, что штрих Шеффера будет эквивалентен отрицанию конъюнкции.
(а/b) ≡ ¬(a & b), т. е. левая и правая части нашего соотношения, будут принимать значение истинности и ложности одновременно. Используя штрих Шеффера, мы можем формализовать пятый тип выводов по Хрисиппу следующим образом:
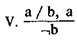
Теперь приведем содержательные примеры на все формулы умозаключений, сформулированных Хрисиппом.
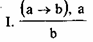
Это мы уже разобрали выше.
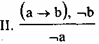
Если у Петрова повышена температура, то он болен. Петров
не болен. Значит, у него температура не повышена.
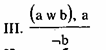
Или мы будем лениться, или будем трудиться. Но мы будем
трудиться. Значит, мы не будем лениться.
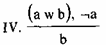
Или мы будем лениться, или мы будем трудиться. Но мы не
будем лениться. Значит, будем трудиться.
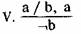
Гений и злодейство несовместимы. Моцарт — гений. Значит, он не злодей.
Теперь мы должны предостеречь против похожих на верные, но ошибочных умозаключений. Выше уже говорилось об ошибках, связанных с тем, что вы делали вывод не от
утверждения антецедента
к
утверждению консеквента,
как учил Хрисипп, а, наоборот, от утверждения консеквента к утверждению антецедента.
Это очень распространенная, весьма досадная ошибка. Если читатель научится не делать хотя бы одной только этой ошибки, можно будет считать, что его труд, затраченный на изучение логики, оправдан. Тем более, если он научится не делать и той ошибки, о которой сейчас пойдет речь.
Ошибка может заключаться в следующем. Вернемся к тому самому Петрову, который, непонятно, то ли болен, то ли нет.
Хрисипп говорит, что если у Петрова повышенная температура, то он болен. Петров не болен. Значит, у него температура не повышена. Здесь отрицается консеквент (в дальнейшем мы будем называть его также следствием), а в выводе отрицается истинность антецедента (мы будем называть его также
основанием).
Значит, вывод делается от отрицания следствия к отрицанию основания:
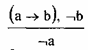
Однако, в практике повседневного мышления мы часто отрицаем антецедент и на этом основании отрицаем консеквент. В данном случае оказывается, что у Петрова нет повышенной температуры, значит, он здоров.
Правы ли мы?
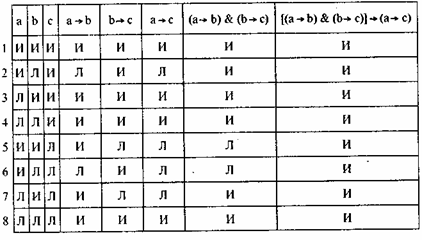
Таблица истинности нам поможет обнаружить ошибку. Вот что получается:
Табл. 22

Схема, по которой получается , что Петров здоров, следующая:
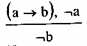
Напомним все умозаключение: если у Петрова повышенная температура (обозначим это высказывание — а), то он болен (высказывание — b). У Петрова нет повышенной температуры (¬а), следовательно, он не болен (¬b). По таблице истинности ищем истинность (а b) и ¬а. Это будет 3-я строчка, в этой же строчке ¬b является ложным. Следовательно, наш вывод о том, что Петров не болен, — ложен. Читатель может возразить, что в 4-й строчке таблицы ¬b является истинным при одновременной истинности (а b) и ¬а. Однако, это уже несущественно. При истинности посылок заключение должно быть всегда истинным, а в 3-й строчке оно уже ложное. Вывод неверен. Быть может, будет более удобен следующий способ проверки правильности умозаключения. Если посылки истинны, то заключение всегда должно быть истинным. Это означает, что всегда должна быть истинна импликация: а, & а,… & ап b. Здесь в антецеденте — конъюнкция всех посылок, а в консеквенте — заключение. Включаем полученную импликацию в Таблицу истинности в качестве ее последней колонки. Если во всех клетках этой колонки для этой импликации получим истинность, это будет означать, что наша импликация является тавтологией, а соответствующее умозаключение — правильным.
Применительно к разбираемому умозаключению со схемой
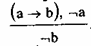 , наша импликация будет иметь вид: [(а b) & ¬a] ¬b.
, наша импликация будет иметь вид: [(а b) & ¬a] ¬b.
Антецедент [(а b) & ¬а], консеквент ¬b. Добавим к нашей таблице колонку [(а b) & ¬а] и колонку [(а b) & ¬а] ¬b, получим:
Табл. 23
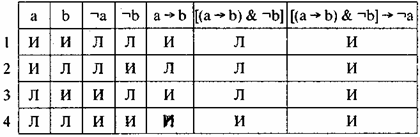
Видим, что в 3-й строчке импликация оказывается ложной, вывод о том, что Петров здоров — неверен.
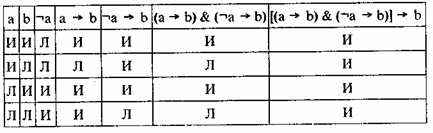
Проверим этим же способом, верен ли вывод: [(а b) & ¬b] ¬а. Снова построим таблицу:
Табл. 24
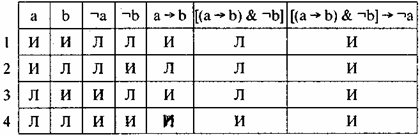
Видим, что во всех строчках последней колонки мы получили Истину. Вывод от отрицания консеквента к отрицанию антецедента верен.
Другое дело — неверный вывод от отрицания антецедента к отрицанию консеквента. Хорошо запомните:
нельзя делать вывод от отрицания основания
(антецедента)
к отрицанию следствия
(консеквента).
Какие ошибки могут быть связаны с использованием третьего типа умозаключений, приведенных Хрисиппом? Рассуждения Хрисиппа связаны с использованием исключающей дизъюнкции. Довольно часто в рассуждениях исключающая дизъюнкция подменяется неисключающей дизъюнкцией. И тогда возникает ошибка. Например, мы можем рассуждать так. Вам сообщили, что тот же Петров является доктором не то физико-математических, не то философских наук. И потом вы узнаете, что Петров — доктор физико-математических наук. Отсюда вы делаете вывод, что он не является доктором философских наук. Это неверно, ибо дизъюнкция здесь не является исключающей. Петров вполне может быть доктором физико-математических наук и доктором философских наук.
Построим таблицу, но предварительно схему Хрисиппа
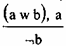
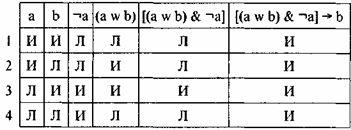
выразим в виде импликации [(a w b) & а] ¬b.
Табл. 25

Заменим исключающую дизъюнкцию на соединительную (неисключающую), которая может быть в ошибочном выводе, и проверим по таблице:
Табл. 26

Видим, что в первой строчке получается ложь, поскольку из истинности основания не следует ложность следствия. Следовательно, рассуждение по III схеме Хрисиппа с заменой исключающей дизъюнкции на соединительную приводит к ошибке.
Рассмотрим четвертый тип вывода или рассуждения, предложенный Хрисиппом:
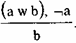
Хрисипп и здесь предлагает исключающую дизъюнкцию. В рассуждениях по этой схеме иногда заменяют исключающую дизъюнкцию на соединительную.
Рассмотрим тот же пример. Если Петров — доктор физико-математических наук или доктор философских наук, а мы обнаружили, что Петров не является доктором физмат наук, то будем иметь полное право считать Петрова доктором философских наук. Это можно проверить по таблице.
IV. Схема Хрисиппа 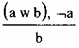 или, в импликативной форме,
или, в импликативной форме,
b [(a w b) & ¬а] b.
Табл. 27
В чем же здесь опасность? Опасность будет заключаться в том, что дизъюнкция может оказаться неполной. Ошибка будет лишь тогда, когда окажется возможным еще какой-то не перечисленный член дизъюнкции. Например, Петров может быть еще и доктором филологических наук. Однако, эта ошибка носит не логический, а фактический характер. Логик вправе предположить, что все члены дизъюнкции перечислены.
В некоторых случаях истинность посылки дизъюнктивного характера может быть установлена на основе чисто логических соображений. Это возможно в тех случаях, когда иные, не перечисленные члены дизъюнкции, логически невозможны. В соответствии с законом исключенного третьего любое высказывание или истинно или ложно. Таким образом, дизъюнкция: “это высказывание истинное или ложное” является полной.
Рассмотрим V тип выводов, отмеченных Хрисиппом
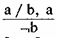
Ошибка здесь чаще всего имеет фактический характер, когда мы предлагаем несовместимость таких суждений, которые на самом деле являются вполне совместимыми. Иногда нам кажется,
что несовместимость двух суждений определена логикой, хотя на самом деле этого нет, и в этом случае мы делаем ошибку, имеющую логический характер.
Например, утверждение, что данное животное — рыба кажется несовместимым с тем, что оно довольно длительное время может жить без воды. Но это вопрос конкретной науки, а не логики. В Австралии обнаружены рыбы, которые могут в течение засушливого периода обходиться без воды.
§ 2. Условные умозаключения. Дилеммы
Исчерпал ли Хрисипп все возможные типы выводов из различных высказываний? Конечно, нет. У Хрисиппа в выводах участвуют только два элементарных высказывания. Существует большое разнообразие различных выводов, в которых участвует более двух элементарных высказываний. И в заключении может быть получено не простое высказывание, а сложное.
Приведем пример условного умозаключения. Если Петров не подготовится к экзаменам, то может получить неудовлетворительную оценку. Если получит неудовлетворительную оценку, то может лишиться стипендии. Если Петров не подготовится к экзамену, то может лишиться стипендии.
Формально это можно выразить следующим образом:
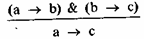
Построим таблицу для проверки истинности этого умозаключения. Здесь три элементарных высказывания, значит, таблица должна содержать 8 рядов (см. табл. 28).
В 8-й колонке мы получили истину в каждой из 8-и строчек. Вывод верен, как это ни прискорбно. Петров может лишиться стипендии.
Конечно, в истинных высказываниях может участвовать два, три и даже очень много импликативных элементарных высказываний.
Могут быть комбинации из разных импликаций, например, такая:
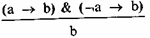
Табл. 28
Проверяем это умозаключение с помощью таблицы истинности и обнаруживаем его правильность:
Табл. 29
Большое значение в рассуждениях, особенно дискуссиях, имеют так называемые дилеммы, которые связаны с использованием комбинаций условных и разделительных посылок. Простая конструктивная дилемма выражается следующей формулой:
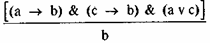
Проверим по таблице истинности:
Табл. 30
Мы установили, что формула в последней колонке является законом логики, т. е. тождественно-истинной формулой. Значит, вывод по схеме нашей дилеммы правомерен. В качестве примера использования дилеммы приведем очень давнюю историю. К знаменитому на всю древнюю Грецию учителю мудрости (их звали софистами) Протагору поступил в качестве ученика некий Эватл. Об оплате они договорились так. Если Эватл выиграет свой первый судебный процесс, он заплатит своему учителю. В противном случае платить не будет. После окончания учебы Эватл обратился в суд с просьбой освободить его от уплаты, рассуждая так: если суд освободит меня от платы за обучение, я платить не буду. Если не освободит, опять таки платить не буду, поскольку я не выиграл судебный процесс. Но я или выиграю судебный процесс, или не выиграю. Значит, я платить не буду. Здесь имеет место дилемма. Протагор ответил ему другой дилеммой с той же структурой, но противоположным выводом: платить будешь! Как это он сделал? Надеемся, что читатель догадается.
Простая конструктивная дилемма состоит из двух посылок. В первой утверждается, что из двух различных оснований вытекает одно и то же следствие. Во второй посылке, которая является дизъюнктивным суждением, утверждается, что одно или другое основание имеет место. В заключении утверждается следствие.
Более сложное умозаключение — сложная конструктивная дилемма. Здесь в первой посылке есть два основания, из которых вытекает соответственно два разных следствия. Вторая посылка утверждает истинность одного или другого основания. В заключении утверждается истинность одного или другого следствия.
Схема такой дилеммы:
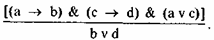
Здесь 4 элементарных высказывания, это означает, что нам потребуется 16 рядов в таблице истинности. Это слишком сложно, чтобы привести здесь всю таблицу. Дотошный читатель в порядке тренировки вполне может убедиться в том, что в последней колонке, состоящей из конъюнкции всех посылок и вытекающих из них следствий, будут все 16 истин.
Приведем пример на такую дилемму.
В пьесе К. Гоцци “Ворон” принц Дженнаро хочет подарить своему брату королю Миллону сокола. Вещие голубки предсказывают несчастье: “В тот же миг, когда Миллону он сокола вручит, Миллона этот сокол мгновенно ослепит. А если не вручит, то будет превращен в холодный мертвый мрамор”. Однако Дженнаро может или вручить, или не вручить сокола Миллону. Значит, или сокол ослепит Миллона, или же он будет превращен в холодный мертвый мрамор.
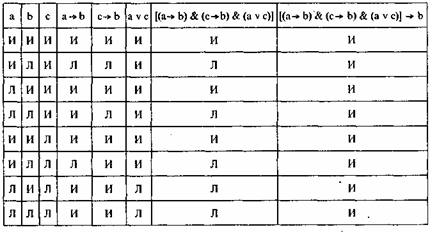
^ Простая деструктивная дилемма
содержит две посылки и заключение. В первой (условной) посылке содержится мысль, что из одного и того же основания вытекают два различных следствия. Во второй посылке содержится дизъюнкция отрицаний этих следствий. Заключение отрицает основание.
Схема простой деструктивной дилеммы:
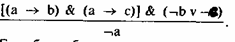 c
c
Если бы он был здоров, то у него была бы нормальная температура. Если бы он был здоров, то у него было бы нормальное давление. Но у него нет нормальной температуры или давление повышено. Значит, он нездоров.
Сложная деструктивная дилемма состоит из двух посылок и заключения. В первой посылке,содержится два условных суждения с различными основаниями и различными следствиями. Во второй посылке содержится отрицание этих следствий в дизъюнктивной форме. Заключение в дизъюнктивной форме отрицания основания двух посылок-.
Формула сложной деструктивной дилеммы:
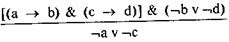
Надеемся, что читатель уже в состоянии подобрать пример на этот вид дилеммы самостоятельно.
Источник
