Задачи вероятность на температуру человека

Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36,8 °С, равна 0,81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется 36,8 °С или выше. ЧипИДейл 6 месяцев назад Подобные задачи приходилось решать при изучении раздела математики, который называется «Теория вероятностей». Из условия задачи важно понять, что оба события (температура меньше 36,8 °С и температура равна или больше 36,8 °С) в терминах теории вероятностей образуют полную группу, а каждое из событий являются противоположными друг другу. В решении данной задачи нам поможет одна из основных теорем, которая доказывает, что сумма вероятностей, составляющих полную группу событий, равна единице. Взяв во внимание, что вероятность температуры ниже 36,8 °С составляет 0,81, и противоположную вероятность обозначив через X, запишем уравнение: 0,81 + X = 1 От сюда вероятность температуры равной или большей 36,8 °С: 1 – 0,81 = 0,19 Ответ на задачу: 0,19 автор вопроса выбрал этот ответ лучшим Artvid 6 месяцев назад Подобные проблемы должны были быть решены при изучении раздела математики под названием «Теория вероятностей». Из условий задачи важно понимать, что оба события (температура ниже 36,8 ° C и температура, равная или превышающая 36,8 ° C) с точки зрения теории вероятностей образуют полную группу, и каждое из событий противоположно друг другу. В решении этой проблемы нам поможет одна из основных теорем, доказывающая, что сумма вероятностей, составляющих всю группу событий, равна одной и той же. Принимая во внимание, что вероятность температуры ниже 36,8 ° C составляет 0,81, и обозначая обратную вероятность через X, запишите уравнение: 0,81 + X = 1 Отсюда вероятность температуры 36,8 ° С или выше: 1 – 0,81 = 0,19 Ответ на проблему: 0,19 Maksimnor 6 месяцев назад Данная задача уж больно простая и лёгкая, с её решением должен справится даже пятиклассник! Если вероятность того, что в случайный момент времени температура тела здорового человека ниже 36,8 равна 0,81 или 81%, то вероятность того, что температура будет 36,8 или выше равна 100%-81%=19%. Ответ на данную задачу 19% или 0,19. Nasos 9 месяцев назад Если вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже чем 36.8 °С, равна 0.81, то вероятность того, что в случайный момент времени у здорового человека температура окажется 36.8 °С или выше равна: 1 – 0.81 = 0.19, или 19% Ответ: 19% Лара Изюминка 5 месяцев назад Задача довольно несложная, но может встретиться как на ОГЭ, так и на ЕГЭ по математике. Итак, для решения нужно вспомнить, что полная вероятность равна 1. Она в данной задача состоит из вероятности того что температура будет наже указанной величины, и той что будет равна или больше указанной величины. Очевидно, нам нужно просто из 1 вычеть вероятность того, что температура ниже, тое есть 1-0,81=0,19. Это и есть искомая вероятность, что равга или больше. Знаете ответ? |
Источник
Есть такое коварное задание в ОГЭ по математике под номером 10 – “Теория вероятности”. С первого взгляда кажется простым, но часто возникают подводные камни и ученики теряют баллы. А задание ведь несложное. На нем баллы набирать надо! Даже если твоя цель – просто перейти порог, прочитав эту статью, сможешь набирать на ОГЭ по математике на 1 балл больше. А если твоя цель – разобраться с самыми сложными задачами этого номера (к сожалению, задачи не всегда элементарные), с этим тоже помогу.
Что такое вероятность
Вероятность – это степень наступления какого-либо события. Вероятность изменяется числом от 0 до 1. Отрицательные числа и числа больше единицы ответом быть не могут!
Как понять результат своего вычисления:
1 – событие точно произойдет (достоверное событие)
от 0 до 1 – произойдет с каким-то шансом, может произойти, а может и нет (случайное событие)
0 – точно не произойдет (невозможное событие)
В ОГЭ мы работаем со случайными событиями, ответ 1 или 0 в 10 задании получиться не может!
Вероятность любого события можно найти по этой формуле:
Формула вероятности
Она решает 80% заданий на ОГЭ, но есть ещё 20%…
Решим самый простой пример:
Пример 1. Самый простой
Объясняю на пальцах:
- 4 бутылки.
- Если 1 бутылка с газом, значит, 3 без газа.
- Нам нужна негазированная, значит, количество благоприятных исходов для нас – 3.
- А всего бутылок 4 – это количество всех исходов.
- Далее решаем по формуле. 3 делим на 4 и переводим в десятичную дробь (ответы на ОГЭ принимаются только в виде десятичных дробей). Получаем 0.75. НИКАКИХ ПРОЦЕНТОВ! Если этого не просят!
Когда событие одно – решить легко, но их может быть несколько… Разберем ВСЁ, что может попасться на экзамене
Кстати, здесь полный разбор досрочного ОГЭ по математике (нажми, чтобы перейти). Объяснение всех заданий!
Сокращенный вариант по математике и разбор досрочного ОГЭ по русскому в этой статье (нажми, чтобы перейти).
Вернемся к вероятностям…
Несовместные события
События А и В несовместные, если они не могут произойти одновременно.
Пример: “получить на ОГЭ по математике 5” и “получить на ОГЭ по математике 4” – это несовместные события. Ты получишь либо 4, либо 5. Ставится только одна оценка.
А как посчитать их вероятность? По формуле:
Формула несовместных событий
Р – это вероятность. Чтобы найти вероятность несовместных событий (наступит или событие А, или событие Б), нужно найти вероятность наступления каждого и сложить их.
Уже немного сложнее, да? Давай решать задачку
Задача на несовместные события
Как проверить, что события несовместные
Задать вопрос: “А могут ли они наступить одновременно?” Если в задаче написано, что Наташа берет наугад 1 пирожок с тарелки, а там их много, она не может взять одновременно 2! Так сказано в условии.
Противоположные события
Два события называются противоположными, если в данном испытании они несовместны и одно из них обязательно происходит.
Формула для расчета:
Формула противоположных событий
Отличие от несовместных
В том, что несовместные события могут и не произойти, а одно из противоположных обязательно произойдет.
Например: “получить на ОГЭ по математике 5” и “получить на ОГЭ по математике 4” – это несовместные события. Но! Ты можешь получить и 3, и 2. Ты получишь 4 или 5 не со стопроцентной вероятностью. Поэтому такие события не являются противоположными.
Противоположное событие – подбросить монету, выпадет либо орел, либо решка. Не выпасть орел или решка не могут! И третьего не дано! Обязательно на какую-то сторону монета упадет, мы не учитываем, что монета упадет на ребро.
Ещё примеры несовместных событий для понимания:
- попасть в мишень и не попасть в мишень
- выздороветь и не выздороветь
- готовиться к экзаменам и не готовиться к экзаменам
Третьего не дано!
С несовместными разобрались, осталось самое сложное…
Независимые события
События А и Б независимы, если появление одного из них не меняет вероятности появления другого.
Пример независимых событий: попасть в мишень при первом выстреле и попасть в мишень при втором выстреле. После первого выстрела стрелок хуже стрелять не стал, мишень не передвинули, ветер сильнее дуть не стал. Поэтому вероятность попадания в обоих случаях одинаковая. Условия одинаковые.
Пример зависимых событий: вытащить из мешка с игрушками мягкую игрушку в первый раз и вытащить мягкую игрушку во второй раз. Вероятность во втором случае изменится, ведь в мешке после первого раза стало на 1 мягкую игрушку меньше (количество благоприятных исходов и количество всех исходов стало на 1 меньше).
Зависимых событий на ОГЭ не дадут, этот пример для понимания независимых)
Решаем сложную задачку
Пример задачи на независимые события
Попасть в мишень(А) и не попасть(В) – это противоположные события. Вероятность Р(А) уже дана в условии. Рассчитываем вероятность Р(В) по формуле.
Попасть в мишень в первый раз и не попасть во второй – это независимые события. Чтобы получить их общую вероятность, нужно перемножить их вероятности по отдельности.
По условию: первый раз попал, второй раз промахнулся, третий раз промахнулся. Перемножаем: Р(А)*Р(В)*Р(В).
Готово!
Теперь ты понимаешь, как решать 10 задание ОГЭ по математике, и даже если тебе попадётся самый сложный номер, ты вспомнишь моё объяснение и заработаешь 1 балл 🙂
Чтобы получать бесплатные уроки по математике и другие авторские материалы для подготовки от онлайн-школы Умскул, подпишись на еженедельную математическую базу знаний ВКонтакте.
А чтобы научиться решать другие задания, подписывайся на наш канал. Мы делимся знаниями, которые сами по себе позволяют подготовиться на хорошие баллы и компенсируют репетиторов. В 2020 году ученики онлайн-школы Умскул набрали на 27,5 баллов больше, чем усредненный балл по России. Проводим бесплатные вебинары каждую неделю. Чтобы получить доступ к материалам, подпишитесь на бесплатную рассылку ОГЭ или ЕГЭ. Присоединяйтесь к нашему блогу и готовьтесь с лучшими!
Кстати, забирай итоговый конспект с нашего занятия 🙂 Вся теория в нем
Итоговый конспект от онлайн-школы Умскул. Преподаватель: Семен Кравченко.
Итоговый конспект от онлайн-школы Умскул. Преподаватель: Семен Кравченко.
Итоговый конспект от онлайн-школы Умскул. Преподаватель: Семен Кравченко.
Также читайте статьи:
Источник
4. Введение в теорию вероятностей
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
(blacktriangleright) Если для выполнения события (C) необходимо выполнение хотя бы одного из двух несовместных (которые не могут произойти одновременно) событий (A) и (B) ((C={A) или (B})), то вероятность события (C) равна сумме вероятностей событий (A) и (B).
(blacktriangleright) Каждое событие можно обозначить в виде круга. Тогда если события несовместны, то круги не должны пересекаться. Вероятность события (C) – это вероятность попасть в один из кругов.
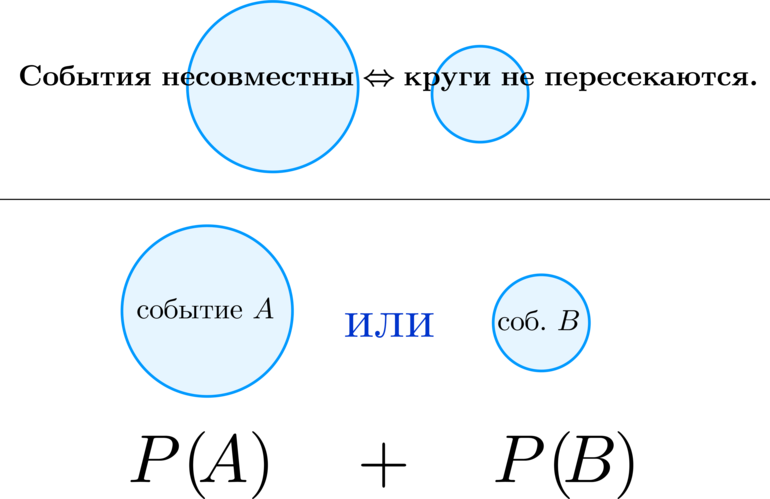
(blacktriangleright) Например, при подбрасывании игральной кости найти вероятность события (C=){выпадет число, делящееся на три}.
Можно сказать, что для того, чтобы выпало число, делящееся на три, нужно, чтобы выпало число (3) или число (6).
Значит, (A=){выпадет (3)}, (B=){выпадет (6)}, причем эти события несовместны!
Тогда (P(C)=P(A)+P(B)=dfrac16+dfrac16=dfrac13).
(blacktriangleright) В случае совместности событий данная формула уже не верна.
Например, при подбрасывании игральной кости найти вероятность события (C=){выпадет четное число}. Ответ должен быть (P(C)=dfrac12).
Но если принять за (A=){выпадет число, делящееся на (2)}, (B=){выпадет число, делящееся на (4)}, то (P(C)=dfrac12+dfrac16ne
dfrac12),
потому что события (A) и (B) совместны: они могут произойти одновременно, когда выпадет (4).
Задание
1
#6381
Уровень задания: Равен ЕГЭ
Два радиста пытаются принять сигнал радиопередатчика, причем вероятность того, что сигнал не будет принят никем, равна (0,08). Найдите вероятность, что хотя бы одному из радистов удастся принять сигнал.
Событие (A=)“хотя бы одному из радистов удастся принять сигнал” означает, что либо первый примет сигнал, а второй – нет, либо второй примет сигнал, а первый – нет, либо оба примут сигнал. Вероятность противоположного события, то есть события (B=)“ни один из радистов не примет сигнал”, равна (0,08). Так как сумма вероятностей противоположных событий равна (1), то (P(A)=1-P(B)=1-0,08=0,92).
Ответ:
0,92
Задание
2
#4018
Уровень задания: Равен ЕГЭ
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме “Вписанная окружность”, равна (0,15). Вероятность того, что это вопрос по теме “Тригонометрия”, равна (0,3). Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Вероятность того, что попадется вопрос по теме “Вписанная окружность” ИЛИ по теме “Тригонометрия”, равна СУММЕ этих вероятностей, то есть [0,15+0,3=0,45]
Ответ:
0,45
Задание
3
#6366
Уровень задания: Равен ЕГЭ
Вероятность того, что новый электрический чайник прослужит больше года, равна 0,9. Вероятность того, что он прослужит больше двух лет, равна 0,82. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Рассмотрим следующий рисунок:

Из рисунка наглядно видно, что, для того чтобы найти вероятность того, что чайник прослужит больше года, но меньше двух лет, нужно из вероятности прослужить больше года вычесть вероятность прослужить больше двух лет.
Иными словами: событие (A) = { Чайник прослужит больше года } состоит из непересекающихся событий (B =) { Чайник прослужит больше двух лет } и (C =) { Чайник прослужит больше года, но меньше двух лет }, т.е. (A = B cup C.) Значит, для вероятностей этих событий можно записать следующее: [P(A)=P(B)+P(C)] Нам нужно найти вероятность события (С): (P(C)=P(A)-P(B)). По условию (P(A)=0,9), (P(B)=0,82), тогда [P(C)=0,9-0,82=0,08.]
Ответ:
0,08
Задание
4
#6367
Уровень задания: Равен ЕГЭ
При изготовлении подшипников диаметром 61 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,976. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше чем 60,99 мм, или больше чем 61,01 мм.
Отметим, что событие “Диаметр подшипника отличается от заданного не больше чем на 0,01 мм” — это тоже самое, что и событие “Подшипник имеет диаметр от 60,99 мм до 61,01 мм”. Вместе события (A) = { Подшипник имеет диаметр меньше чем 60,99 мм }, (B) = { Подшипник имеет диаметр больше чем 61,01 мм }, (C) = { Подшипник имеет диаметр от 60,99 мм до 61,01 мм } составляют вообще все возможные варианты, значит, сумма их вероятностей равна 1:[P(A)+P(B)+P(C)=1.] По условию нам нужно найти вероятность события, которое является объединением событий (A) и (B), а значит искомая вероятность равна сумме их вероятностей:[P(A)+P(B)=1-P(C)] [P(A)+P(B)=1-0,976=0,024.] Для наглядности приведем рисунок:

Ответ:
0,024
Задание
5
#6368
Уровень задания: Равен ЕГЭ
Вероятность того, что на тестировании по истории учащийся Т. решит больше 10 задач, равна 0,75. Вероятность того, что Т. верно решит больше 9 задач, равна 0,8. Найдите вероятность того, что Т. верно решит ровно 10 задач.
Для наглядности нанесем данные из условия на прямую:

Тогда видим, что событие (A) = { Решил больше 9 задач } состоит из объединения несовместных событий (B) = { Решил больше 10 задач } и (C) = { Решил ровно 10 задач }, а значит, его вероятность равна сумме вероятностей: [P(A)=P(B)+P(C).] Так как требуется найти вероятность события (C), то (P(C)=P(A)-P(B)), то есть [P(C)=0,8-0,75=0,05.]
Ответ:
0,05
Задание
6
#6369
Уровень задания: Равен ЕГЭ
Вероятность того, что в случайный момент времени температура тела здорового человека окажется ниже (36,8^{circ}mathrm{C}), равна 0,81. Найдите вероятность того, что в случайный момент времени у здорового человека температура окажется (36,8^{circ}mathrm{C}) или выше.
Рассмотрим рисунок:

События “Температура тела ниже (36,8^{circ}mathrm{C},)” и “Температура тела выше или равна (36,8^{circ}mathrm{C},)” противоположные, значит, сумма их вероятностей равна 1. Тогда искомая вероятность равна: [1-0,81=0,19.]
Ответ:
0,19
Задание
7
#6370
Уровень задания: Равен ЕГЭ
Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 16 пассажиров, равна 0,96. Вероятность того, что окажется меньше 10 пассажиров, равна 0,55. Найдите вероятность того, что число пассажиров будет от 10 до 15.
Для наглядности решения начертим рисунок:

Отсюда видим, что событие (A) = { В автобусе окажется меньше 16 пассажиров } состоит из двух непересекающихся событий (B) = { В автобусе окажется меньше 10 пассажиров } и (C) = { В автобусе окажется от 10 до 15 пассажиров }, значит, для вероятностей можно записать: (P(A)=P(B)+P(C)). Так как нам нужно найти вероятность события (C), то: [P(C)=P(A)-P(B)=0,96-0,55=0,41.]
Ответ:
0,41
Задания на нахождение суммы вероятностей несовместных событий — обязательная часть ЕГЭ по математике. Знать алгоритм их решения и уметь его применять должны все выпускники вне зависимости от уровня их подготовки. При этом, как показывает статистика, задачи ЕГЭ, в которых требуется вычислить сумму вероятности несовместных событий, вызывают у старшеклассников определенные трудности. Восполнить пробелы в знаниях вам поможет образовательный портал «Школково». Там представлены задачи на нахождение суммы вероятностей двух несовместных событий, подобные тем, что встречаются в ЕГЭ. Разобравшись с алгоритмом их решения, учащийся сможет успешно преодолеть аттестационное испытание.
Важно запомнить!
При решении подобных задач необходимо руководствоваться следующими теоретическими данными:
- Случайным называется то событие, исход которого невозможно предсказать до его свершения. В качестве примера можно привести следующие действия: подбрасывание монеты или игральной кости, выигрыш лотерейного билета и т. п.
- Вероятность случайного события равняется отношению числа благоприятных исходов к общему числу исходов. Очевидно, что ее значение не может превышать 1.
- Несовместными называются два события, которые не могут произойти единовременно в результате проведения случайного эксперимента.
Какие еще важные моменты стоит отметить в этой теме? При решении подобных задач в ЕГЭ необходимо вспомнить теорему вероятности суммы двух несовместных событий. Ее формулировка звучит следующим образом. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
Записать ее можно таким образом:
(P(A+B)=P(A)+P(B)), где (A) и (B) — несовместные события.
Замечание. Вероятность суммы несовместных событий будет равна сумме их вероятностей, даже если речь идет о попарно несовместных событиях.
Как подготовиться к экзамену?
Для того чтобы задания по теории вероятности профильного уровня не вызывали у вас затруднений, рекомендуем воспользоваться информацией на образовательном портале «Школково». Здесь представлена формула вероятности суммы несовместных событий, базовые теоремы и другой теоретический материал, который поможет вам подготовиться к ЕГЭ. Кроме того, в соответствующем разделе собраны упражнения для отработки полученных знаний. Для каждого задания наши специалисты прописали алгоритм решения и привели правильный ответ. Выпускники имеют возможность практиковаться в выполнении упражнений различного уровня сложности в режиме онлайн.
Источник
